| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 코드워
- scala
- golang
- 자바
- boj
- OOM
- 튜토리얼
- codewars
- dynamic programming
- 스칼라
- 리눅스
- leetcode
- Linux
- zookeeper
- go
- docker
- 동적프로그래밍
- 알고리즘
- 프로그래머스
- programmers
- 문제풀이
- redis
- HBase
- Java
- Go언어
- 주키퍼
- gradle
- Python
- 파이썬
- DP
- Today
- Total
파이문
Triangle number check 본문
Triangle number check
항상 파이썬으로 풀지만 오늘은 자바를 공부할 겸 자바로 풀어보았습니다.
입력 받은 n이 삼각형이 되는 수인지 판별 하면 되는 문제였는데요, 여기서 삼각형이란 삼각형 모양을 의미합니다. 삼각수? 정도로 생각하면 될 것 같아요. 운이 좋게도 바로 얼마전 우연히! 프로젝트 오일러 41번이였나, 42번 문제를 보았는데 삼각수가 나왔었거든요.
그래서 쉽게 삼각수 문제라는 것을 유추해내고 공식만 대입하였습니다.

이는 n번 째의 삼각수는 N 이라는 의미입니다.
즉 첫 번째 삼각수는 1, 두 번째 삼각수는 1-2-3이니 2 * (2+1)/2 해서 3 (마지막 수죠), 세 번째 삼각수는 6(3 * 4 / 2)이 되는 거죠.
다시 말하면 순서는 n이고 삼각수는 N이 되는 것이죠.
그래서, 입력 받는 number가 n(n+1)/2가 되는지 확인해보면 됩니다.
제가 처음에 생각한 것은 인수분해를 통해서 나온 n 값이 정수인지 아닌지를 판별하는 것이었습니다.
테스트 케이스는 돌아가서 submit 했지만 통과를 못하더군요 ㅠㅠ
에러는 expected:
결국 다른 사람의 코드를 보았고, 제 소스에서 논리적인 결함이 있다는 사실을 알게 되었습니다. (그게 뭘까요. 오늘은 시간이 없어서 주말에 알아보기로....)
처음 작성한 코드는 다음과 같습니다.
public class TriangleNumbers {
public static Boolean isTriangleNumber(long number) {
if (number == 1 || number == 0) {
return true;
}
double a = (-1 + Math.sqrt(8 * number)) / 2;
double b = (1 + Math.sqrt(8 * number)) / 2;
double alpah = Math.round(a * 100);
double beta = Math.round(b * 100);
if((alpah / 100) % 1 == 0.0 || (beta / 100) % 1 == 0.0 ){
return true;
}
return false;
}N 이 n * (n+1) / 2이기 때문에 전체를 n에 관한 다항식으로 정리 후, 인수분해 해서 해의 값 a와 b를 만들었구요. 이 때, a와 b가 정수이면 입력받은 number가 삼각수라고 생각하였습니다. 중간에 100을 곱하고 나누는 이유는 분명 답이 정수가 나올거라고 예상했는데 실수가 나와서 (예를 들어서 4가 3.99 이하로 나오더군요. 아마 자바에 대한 미숙? 오차? 때문에 그런 것 같습니다.) 이를 해결하기 위해 위와 같은 과정을 추가하였습니다.
제 테스트코드에선 돌아가지만 통과를 못한거보면 논리적인 오류가 있다는 의미였겠죠.. 그래서 인터넷을 막 뒤져서 소스 하나를 찾았습니다.
제가 찾은 소스는 바로 이것입니다.
public class TriangleNumbers {
public static Boolean isTriangleNumber(long number) {
long sqrt = (long) Math.sqrt(8 * number + 1);
return (sqrt * sqrt == 8 * number + 1);
}
}엄청 간결합니다.
무슨 의미인걸까 하나씩 뜯어보았어요.
일단 밑의 코드에 하나씩 수를 대입하니까 놀랍게도 삼각수는 8을 곱하고 더하기 1을 하면 제곱근이 되더군요. 와우.
그래서 위키피디아를 찾아봤는데 띠링!
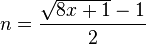
이 공식이 있습니닷 ㅎㅎ..
원문은 이렇게 쓰여있네요.
Triangular roots and tests for triangular numbers[edit]
By analogy with the square root of x, one can define the (positive) triangular root of x as the number n such that Tn = x:[6]
which follows immediately from the quadratic formula. So an integer x is triangular if and only if 8x + 1 is a square. Equivalently, if the positive triangular root n of x is an integer, then x is the nth triangular number.[6]
어찌됐든 문제 하나 겨우 풀었습니당 ㅠㅠ
이를 통해 깨달은게 있다면, 수학 공부를 열심히 하자 ㅠㅠ 문서를 제대로 읽자 ㅠㅠ 마지막으로 코드워에서 푼 모든 문제를 깃허브에 올려야겠다는 생각이었습니다. 귀찮아서 그냥 블로그에만 포스팅하였는데 코드 정리겸, TIL을 실행할 겸 이번 주말에 몰아서 올리려구요.
(근데 이 코드도 submit시 타임 아웃이 뜨더라구요. 좋은 알고리즘이란게 뭘까요... 자바라 그런건지 아님 훨씬 효율적인게 있는건지..)
'문제 풀이 > codewars' 카테고리의 다른 글
| Consecutive strings (0) | 2016.04.10 |
|---|---|
| Valid Phone Number (0) | 2016.04.10 |
| Replace With Alphabet Position (0) | 2016.04.02 |
| Find The Parity Outlier (0) | 2016.04.02 |
